In the previous issue, I presented the Restricted Boltzmann Machines, which were introduced by Geoffrey Hinton, a professor at the University of Toronto, in 2006, as a method for speeding up neural network training. In 2007, Yoshua Bengio, professor at the University of Montreal, presented an alternative to RBMs: autoencoders.
Autoencoders are neural networks that learn to compress and process their input data. After the processing that they do, the most relevant features of the input data are extracted and they can be used to solve our machine learning problem, such as more easily recognizing objects in images.
Usually autoencoders have at least 3 layers:
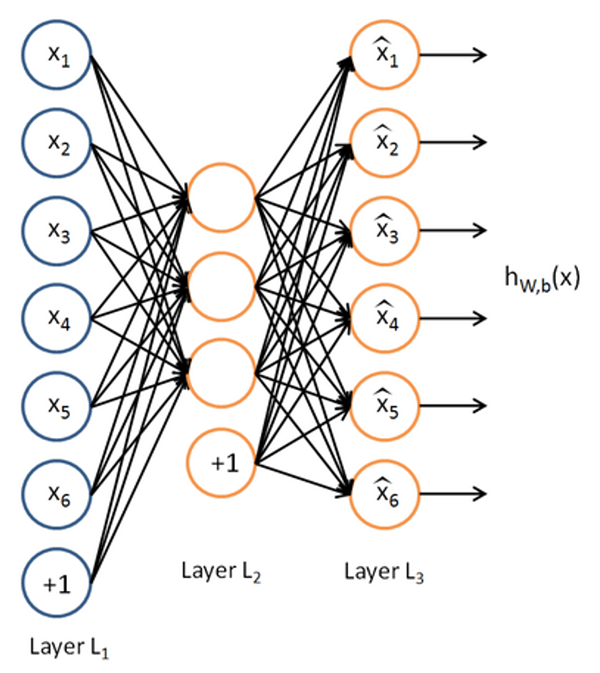
The values of the output layer in an autoencoder are set to be equal to the values of the input layer (y = x). The simplest function that does this "transformation" is the identity function, f(x) = x.
For example, if we have an input layer with 100 neurons, but on the middle layer we have only 50 neurons, then the neural network will have to compress the input data, because it can"t memorize 100 uncompressed values with only 50 neurons. If our input data is completely random, then this is not possible and there will be errors in reproducing the input data. However, if our data has some structure, for example it represents the pixels of a 10x10 image, then we can get a more compressed representation of the pixel. If a pixel in an image is green, the 8 surrounding pixels are also greenish. If there are pixels of the same color on a circle, instead of remembering the position of each pixel (for a circle of radius 4 this would mean about 25 values), it is enough to know that at position x, y we have a circle of radius r, which can be stored with only 3 values.
Of course, such a level of compression won"t be achieved using only one layer. But if we stack several autoencoders, as we did with Restricted Boltzmann Machines to get Deep Belief Networks, we will get more and more compact features.
If we treat each layer as a function that receives as input a vector and returns another one, that has been processed, then in a 3 layer autoencoder we have 2 functions (the first layer, the visible one, just sends its inputs to the next layer).
The first function will do the encoding of the input:
h=f(x)=sf(Wx+bh)
where sf is a nonlinear activation function, used by the hidden layer, W represents the weights of the connections between the visible layer and the hidden one, while bh is the bias unit for the input layer.
The second function will decode the data:
y = g(h) = sg(W"x+by)
where the constants have a similar meaning, but they are between the hidden layer and the output layer this time.
The combination of the two functions should be the identity function, but if we take only the encoding function, we can use it to process our data to get a higher level representation.
To quantify the error we make with regard to the identity function, we can use the L2-norm of the difference:
L(x, y) = ||x-y||2
The parameters of the autoencoder are chosen as to minimize this value.
The model presented above represents a classical autoencoder, where the learning of relevant features is done by compressing data, because the hidden layer has fewer layers than the input one.
There are other types of autoencoders, some of them even with more neurons on the hidden layer than on the input layer, but which avoid memorization using other methods.
Sparse autoencoders impose the constraint that each neuron should be activated as rarely as possible. The hidden layer neurons are activated when the features they represent are present in the input data. If each neuron is rarely activated, then each one has a distinct feature. In practice this is done by adding a penalty term for each activation of a neuron on the input data:

where β controls the amount of penalty for an activation, ρj is the average activation of neuron j, and ρ is the sparsity parameter which represents how often we want each neuron to be activated. Usually it has a value below 0.1.
Denoising autoencoders have another approach. While training the network, some of the input data is corrupted, either by adding gaussian noise, or by applying a binary mask, that sets some values to 0 and leaves the rest unchanged. Because the result of the output layer is still the original, correct values, the neural network must learn to reproduce the correct values from the corrupt ones. To do this it must learn the correlations between the values of the input data and use them to figure out how to correct the distortions. The training process and the cost function are unchanged.
Another variant of autoencoders are contractive autoencoders. These try to learn efficient features by penalizing the sensibility of the network towards its inputs. Sensibility represents how much the output changes when the input changes a little. The smaller the sensibility, the more similar inputs will give similar features. For example, let`s imagine the task of recognizing handwritten digits. Some people draw the 0 in an elongated way, others round it out, but the differences are small, of only a couple of pixels. We would want our network to learn the same features for all 0s. Penalizing the sensibility is done with the Frobenius norm of the Jacobian of the function between the input layer and the hidden one:

All these models can be combined, of course. We can impose both sparsity constraints and corrupt the input data. Which of these techniques is better depends a lot on the nature of the data, so you must experiment with various kinds of autoencoders to see which gives you the best results.
There are other types of autoencoders, such as Transforming Autoencoders or Saturating Autoencoders , but I won"t give more details about them now, instead I will show you how to use autoencoders using Pylearn2 , a Python library developed by the LISA research group from the University of Montreal. This library was used to develop several state of the art results, especially related to image classification.
In Pylearn2, deep learning models can be configured using YAML files, which are then executed by the train.py runner from the library, which does the training and then saves our neural network into a pickle file.
!obj:pylearn2.train.Train {
dataset: !pkl: "cifar10_preprocessed_train.pkl",
model: !obj:pylearn2.models.autoencoder.ContractiveAutoencoder {
nvis : 192,
nhid : 400,
irange : 0.05,
act_enc: "tanh",
act_dec: "tanh",
},
algorithm: !obj:pylearn2.training_algorithms.sgd.SGD {
learning_rate : 1e-3,
batch_size : 500,
monitoring_batches : 100,
monitoring_dataset : !pkl: "cifar10_preprocessed_train.pkl",
cost : !obj:pylearn2.costs.autoencoder.MeanSquaredReconstructionError {},
termination_criterion : !obj:pylearn2.termination_criteria.MonitorBased {
prop_decrease : 0.001,
N : 10,
},
},
extensions : [!obj:pylearn2.training_algorithms.sgd.MonitorBasedLRAdjuster {}],
save_freq : 1
}
Autoencoders represent a way of taking a dataset and transforming it in such a way as to obtain a more compressed and more discriminative data set. Using the latter we can then solve our problem in an easier manner, be it a regression, clustering or a classification problem.
In the next article, I will start presenting the improvements used in Deep learning with regard to layers and we will see several kinds of layer types.
by Ovidiu Mățan